One of the most powerful features of After Effects is the ability to work with 3D layers and a virtual camera. While it is simple to add a camera to a composition and animate it, greater creative control over the end result can be achieved with a basic technical understanding of how cameras work, and what the various settings mean.
The aim of this article is to try and bridge some of the gaps between the creative and technical aspects of the After Effects camera. It is probably most useful for those writing scripts and expressions that use the camera settings. If you want to skip to the end, then there are a few copy & paste expressions on the last page.
When you’re using a virtual camera – in any graphics application, not just After Effects – it can be confusing to understand the slightly different terminologies in use. Unfortunately there are several cases where different applications use different names for the same thing, so to begin with we’ll run through the basic principles of cameras and then we’ll discuss the way they apply to After Effects.
Background – Real Cameras 101
At the most basic level, a camera is a lens that focuses an image onto a surface. The simplest type of camera is a “camera obscura”, which is basically a box with a hole in it. There are a few famous examples of camera obscuras open to the public, and recently there’s been a lot of attention given to the theory that the Dutch artist Vermeer used one to compose his paintings.
Camera obscuras don’t offer any control over the image they produce, and so one of the biggest advances with the invention of the modern camera was the introduction of a lens to replace the small hole.
The lens is the most fundamental control we have over an image produced by a camera. The lens governs exactly how much of an overall scene is ‘captured’ or recorded. Choosing a lens, and describing the attributes of a given lens, is one of the most important parts of working with cameras.
Most of this article is about measuring and controlling the camera lens, but while it’s easy to list the maths involved, it’s far more difficult to explain the creative importance that a lens has when using a camera. There are many resources available the explain the way that different lenses perform, and professional photographers spend a lot of time discussing and comparing real-world lenses that can cost tens of thousands of dollars.
Wikipedia is as good a place as any for an overview of the effect that different lenses can have on an image, and there are many other similar resources that focus on the creative side.
So before we delve into it, trust me – the lens is a big deal.
Understanding – and misunderstanding – perspective foreshortening
There are many creative reasons for choosing a particular lens, but there’s one thing that’s often taught about lenses which is slightly wrong.
In practically all photography textbooks you will find some sort of statement about how telephoto lenses compress the background, or that wide angle lenses increase the apparent distance between objects, or something to that effect. It doesn’t matter how the statement is worded, it’s generally taught that the lens you choose will determine how close objects appear together.
This is not exactly right. It’s not completely wrong, either, but the lens is only half the equation. Understanding this misunderstanding is important when animating a camera.
If you frame the same shot with a wide angle and a telephoto lens, then they will indeed look different. As the textbooks say, the telephoto version will look “flatter”, and objects will appear closer together than they do in the wide angle version. This difference is one of the key creative considerations when choosing or animating a lens.
Here’s an example from After Effects, where 7 rectangles have been arranged in 3d space, each of them 200 pixels apart. The same composition has been rendered out with 3 different camera lens settings – 24mm, 50mm and 135mm.

You can clearly see the difference. And so it would appear that the textbooks are correct – compared to the lens in the middle, the wide angle lens has increased the distance between the rectangles, while the telephoto lens has flattened them together.
So if the effect is real, why are the textbooks slightly wrong?
The answer is because it’s not just the lens itself. It’s actually the different distances from the camera to the subject matter – when the lens is changed, the camera position changes too in order for the framing to stay the same.
If we consider three lenses – a wide angle lens, a telephoto lens, and a “normal” lens that is in between – then every time we change between these lenses that camera will see a different result. The wide angle lens will show us more of the scene than the “normal” lens and the telephoto lens will show us less.
But changing the lenses changes the framing of the shot – and that’s not what we said we’re doing. We said we’re framing all three versions the same, and in order to do that we need to move the camera to compensate for the different lenses. We need to move the camera forward when we use the wide angle lens, and backwards when we use the telephoto lens.
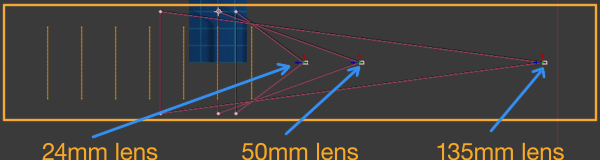
Side view of the scene, showing the 3 camera positions and the 7 rectangles.
By the time we have framed up our scene so that the three shots look the same, our camera is in three different positions.
It’s the difference in the relative position of the subject matter to the camera’s position that causes the shots to look different, not just the lens itself.
As I said earlier – the difference in perspective is there, and this is something that is often used as a tool by photographers. Two objects which are very far away can be made to appear a lot closer by shooting them with a telephoto lens from a far distance. It’s something that is often taken advantage of in films, when the safety of the actor is important.
For example – in the freeway scene from the film Bowfinger, Director Frank Oz needed to create the impression that Eddie Murphy was surrounded by speeding cars. By shooting the closeups and cutaways from a long way away but using a powerful telephoto lens, the cars could be a safe distance away from Murphy while appearing to be very close. This meant the close ups and cutaways could be filmed in-camera, without the need for either a stunt double or additional expensive greenscreen visual effects.
The idea that lens choice governs how foreground and background objects appear is so pervasive that it’s easy to overlook that it’s actually the relationship between lens choice and the distance to the camera which is important.
The distance from the subject matter to the camera needs to be considered for unusually tall or narrow compositions. If a wider angle lens is used with the camera close to the scene, then the sides of the scene will show warping and distortions because they’re a lot further away from the camera than the middle. The solution to this problem is to move the camera further away and use a less-wide lens, so the objects at the edges of frame are a more similar distance to the camera as the ones in the centre.

Measuring up
Most people are familiar with the idea of wide angle and telephoto lenses, and also zoom lenses which allow the operator to adjust the lens manually. Beyond these simple terms, however, professionals need to be able to describe a lens with more precision.
While the terms “wide angle” and “telephoto” are broadly used, there are two more technical methods used to precisely describe and measure the characteristics of a lens.
In traditional photography – in other words when we have a real camera – the convention is to describe the lens in terms of mm, this is a measurement of the distance between the first lens element and the surface the image is focused onto.
Because we’re referring to a physical distance, this is known as the focal length of a lens. You might see a lens described as a 50mm lens, or a 28mm lens – this is the focal length. A 50mm lens means the lens is 50mm from the image sensor, which these days is a microchip but in the old days was a strip of film. It’s a very literal terminology.
For the purposes of this article, I’ll use the term “image plane” to refer to the point where the camera records the image. As stated above, the “image plane” could be a strip of film in a camera, the paper in a polaroid camera, the CCD in a digital camera or your phone, or the wall in the San Francisco bridge camera obscura. It’s basically where the picture we’re taking is focused.
So the focal length of a lens is the distance from the lens to the image plane.
A zoom lens allows us to change the focal length, by physically moving the lens further away or closer to the image plane. A zoom lens will be described by the smallest to largest focal lengths it covers, for example a 28 – 80mm zoom. In this case, the lens will physically slide between 28mm from the image plane, up to 80mm. This is why zoom lenses extend when you change the setting.

The closer the lens is to the image plane, the wider the image – in other words, the more you see.
The further away the lens is, the more you are magnifying the scene. You don’t see as much to the sides. A telescope is an extreme version of a telephoto lens.
So a wide angle lens has a small focal length, and a telephoto lens has a long focal length.
This is one reason why telephoto lenses are so long – when you see sports photographers or even paparazzi with big long telephoto lenses, it’s because the glass lenses are so far away from the image sensor – these lenses have a very long focal length.
Photographers and Directors of Photography also use this as a form of jargon – you’ll often hear a DOP say something is “shot on a long lens”.
Optical Geek Speak
Photographers have been happily describing their lenses by their focal length for over 100 years. But when the geeks got involved and began to work out the science and mathematics of optical systems, they started using a different system.
Instead of describing a lens by its focal length in millimeters, the mathematicians preferred to describe the angle that a lens captured in degrees. This is referred to as either the angle of view or the field of view – most of the time these terms mean the same thing.
(In photography the angle of view is always measured in degrees, but in some specific scientific applications the measurement may be listed using sexagesimal notation – that’s the one with minutes and seconds, most commonly associated with latitude and longitude.)
This is a precise measurement of the angle of a scene that the lens can capture, as if measured by an imaginary protractor on top of the lens. A wide angle lens will capture a large viewing angle, so it has a large angle of view. A telephoto lens will have a narrower viewing angle, so the angle of view will be smaller.
So when it comes to describing a camera’s lens, we already have two alternative ways of doing it. Photographers measure the focal length in mm, while mathematicians measure the angle that the lens can capture in degrees, referring to it as either the angle of view or the field of view.
Terms of confusion
It would be nice to think that we simply have two different approaches to measuring the same thing, and that converting a focal length in mm to an angle of view in degrees would be as simple as converting from Celsius to Fahrenheit.
Unfortunately, neither of these techniques is that simple, and both approaches involve some type of ambiguity. So let’s examine how these two approaches are more complex than they seem.
How do you solve a problem like mm
When you describe a lens by its focal length, you are recording a very literal, real-world physical measurement. A 50mm lens is literally 50mm away from the image plane, and in this regard there is no confusion or ambiguity.
The problem with this approach is that the same focal length gives a different result with image planes of different sizes. The same lens can be considered a telephoto lens if the image plane is small, or a wide-angle lens if the image plane is large.
When photographers used to shoot on film, this wasn’t a problem because just about every photographer everywhere was shooting on the same size film – 35mm. 35mm film was the defacto standard, and the only people using different sizes – such as 70mm medium format film – were professionals who understood what they were doing.
So for as long as 35mm film was the most popular format for photography, describing lenses by their focal length in mm worked pretty well because everyone could safely assume the focal length was relative to the same size image plane.
But these days photography is now dominated by digital cameras, and the image sensors used come in many different sizes. There are a few digital cameras that have an image sensor the same size as 35mm film, but in general there are several different sizes available, and so the same lens will give different results on different cameras.
This means that the focal length alone is not enough to describe how a lens will perform, we also need the size of the image plane to know if the lens is wide angle or telephoto.
So that’s the problem with describing a lens by focal length: although measuring its focal length in mm gives us a real-world measurement, we can’t use the focal length alone to predict how the lens will perform unless we know the size of the image plane as well, and this varies between different cameras.
The only way is up, down or across
Describing a lens by measuring its angle of view might seem like a better option, but unfortunately this approach also has problems.
Because photographic lenses are circular, they generate a circular image. It doesn’t matter if the lens is a hole in a shoebox or an expensive piece of glass with autofocus and image stabilization – it will produce a circular image.
If we were producing circular images then measuring a lens by its angle of view would be easy, as one of the defining attributes of a circle is that it has the same diameter in all directions. No matter which way we measure a circle, it has the same width – which equates to the same angle of view.
The problem is that photographs, films and TV shows have always been produced as rectangular shapes. It doesn’t matter if the camera is recording the image onto film, polaroid photo paper or a digital image sensor – in all real-world cases the circular image that comes out of the lens is cropped into a rectangular shape.
There are many different formats, sizes and aspect ratios that are in use across so many different fields and disciplines. Even if we only look at film and television there are several different aspect ratios to consider- from the original 1 : 1.3 aspect through to the current Panavision widescreen aspect of 1 : 2.39
When we look at a rectangle as opposed to a circle, such as the standard 16:9 aspect ratio used for television, there are three different axis that can be measured as the ‘angle of view’ – horizontal, vertical, and diagonal.
This means that simply having an “angle of view” is not enough to know how a lens will perform, we also need to know if the measurement is horizontal, vertical or diagonal. There is no general standard for which is preferred – and when we have extreme aspect ratios the difference between them can be very large. Mathematicians, computer programmers, scientists and technicians all vary in their preference for measuring the angle of view – even different 3D engines used in computer games use different settings – some horizontal, some diagonal.
So that’s the problem with the “angle of view” – once again the raw number is not enough, we also need to know whether the measurement is horizontal, vertical or diagonal. This is directly relevant when trying to match the camera settings in After Effects with those from another application.
It’s tradition
We can summarise everything so far:
1) The lens is a fundamental creative tool.
2) The relationship between the lens and camera’s position determines the composition of the shot.
3) Lenses are measured either by their focal length (in mm) or by their angle of view (in degrees).
4) Both of these measurements need additional information before we can predict the output of the lens.
5) The focal length of a lens is measured in mm, but we need to know the size of the image plane before we can tell if the lens is wide angle or telephoto.
6) The angle of view is measured in degrees, but we also need to know if the measurement is horizontal, vertical or diagonal.
What’s just as important as understanding these differences is also understanding how these terms have been used throughout the history of photography.
Until very recently, 35mm film has been the dominant film format used in stills photography. The 35mm film format is very old – it was developed in the 1890’s – and became the official standard for cinema in 1909.
While early cinema cameras ran the film vertically through the camera and recorded an image with an aspect ratio of 1 : 1.3, the popularity of the film size meant that many manufacturers experimented with adapting it for use with stills cameras. By spooling the film through the camera horizontally, instead of vertically, a larger image could be captured than with a cinema camera. As early as 1914 a stills camera had been developed that captured an image size of 36mm x 24mm onto strips of film that were 35mm wide, however there were many different variations offered by different companies.
In 1925 Leica released a camera that recorded an image size of 36mm x 24mm onto 35mm film and it became incredibly popular – and by the 1950s that size was the most popular film format in use by photographers worldwide.
Since then, the term “35mm photography” has become synonymous with recording an image size of 36mm x 24mm, and for at least 50 years the format has been so ubiquitous that all camera and photographic equipment was assumed to be for 35mm photography unless specifically stated. This included lenses.
Because photographers assumed that everyone was shooting 35mm film and recording an image size of 36mm x 24mm, lenses were only described by their focal length and generations of photographers learned how these numbers related to the images they produced.
At some point, someone claimed that a 50mm lens produced an image that matched what the human eye could see (when shooting 35mm film). This claim has been repeated so many times for so long that’s it’s become some type of photographic institution. If you pick up a book on photography then it’s a safe bet it will be in there somewhere.
While the idea that a 50mm lens is comparable to the human eye isn’t true – and there are many website articles and discussions on the topic – the 50mm lens is considered a “standard”, or “normal” lens. This basically means that it isn’t a wide-angle lens or a telephoto lens, it’s in the middle. It’s just normal.
The 50mm lens is something of a photographic benchmark. It is shorthand for “normal”. It is considered the starting point, or reference point, for all other lenses.
With a 50mm lens considered “standard”, anything with a smaller focal length is considered wide angle and anything larger is considered telephoto. Over time, specific focal lengths have become popular and are considered staple tools for the photographer.
35mm and 28mm lenses are popular wide-angle lenses, while lenses with focal lengths between 80 and 105mm are often referred to as a “portrait” lenses, because they’re so popular with photographers shooting portraits. This is worth commenting on as well, because many photography books will claim that lenses with focal lengths of around 80 – 105 mm are popular with portrait photographers because they slightly flatten the face, which makes people look more attractive.
This is a more specific version of the same claim about perspective that we looked at earlier, and once again the complete explanation has to do with the camera’s position. If a photographer has to shoot a portrait with a normal 50mm lens or wider, then they need to be very close to the person they’re shooting. This is not only uncomfortable for all involved but may also lead to practical issues with lighting and shadows. If the photographer uses a lens that is much longer than 105mm, then they will have to be several metres away from the subject – something that is not possible in small studios and even if it is, does little for intimacy. Using a lens with a focal length between 80 and 105mm means the photographer is a comfortable and practical distance from the subject – hence their popularity.
It is true that with the same framing, a portrait shot with a 105mm lens will look “flatter” than one shot with a 50mm lens, but the more flattering appearance of the subject is only half the explanation for the longer lens being the preferred option. A 400mm lens might be even more flattering, but it’s not that useful if the photographer has to stand 10 metres away.
When the numbers get really low the lenses produce the distinctive “fisheye” effect, and when they’re really high the camera is like a telescope – an effect used as a narrative device by Alfred Hitchcock in the film “Rear Window”.
As digital photography has overtaken 35mm film, photographers still refer to lenses relative to the way they perform with 35mm film, even though the size of the digital image sensor may be different. Some manufacturers will give a “conversion factor”, or “crop factor” so that the number used to describe a lens can be translated to the 35mm industry standard.
For example, a Canon APS-C lens has a conversion factor of 1.6. This means that a 31.25mm lens on an APS-C camera will produce the same image as a 50mm lens on a 35mm camera (31.25 x 1.6 = 50), or that a 50mm lens on an APS-C camera is equivalent to an 80mm lens on a 35mm camera (50 x 1.6 = 80).
After Effects – into the virtual world
3D layers and the After Effects camera were introduced with version 5, in 2001. Like real-world cameras, the virtual camera in After Effects also comes with a virtual “lens” that can be zoomed in and out.
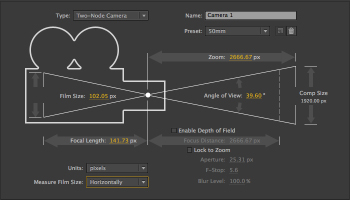
Since version 5 in 2001, the After Effects camera has seen gradual improvements and some additional controls and settings. The various parameters in After Effects directly relate to their real-world equivalents but while the underlying principles are the same as real-world photography, there are a few important considerations to make.
Firstly, After Effects operates with pixels. It doesn’t work with measurements such as mm, inches or metres.
Secondly, After Effects follows decades of tradition and uses 35mm photography as its reference for lens presets.
In the After Effects timeline, the camera “lens” is controlled by the “zoom” parameter, which is measured in pixels. We can think of the zoom parameter as being equivalent to the focal length – smaller values give us a wider view and larger values allow us to zoom in.
When we go to the camera settings, however, we are also offered a list of preset lenses, listed by their focal length in mm. Selecting one of these presets results in the zoom parameter being set to the After Effects equivalent in pixels.
After Effects also shows us the equivalent angle of view, measured in degrees. We can specify if the measurement is to be made horizontally, vertically or diagonally.
Earlier versions of After Effects did not explicitly explain that the lens presets related to 35mm photography, but current versions also allow you to change the ‘film size’, and specify measurements in different units.
Even if you enter in a custom film size, as soon as you select a lens preset those values will be changed back to 36mm x 24mm – the dimensions of a 35mm film photograph.
If you add a new camera with a wide-angle lens, After Effects positions the camera closer to the composition and if you add a new camera with a telephoto lens, the new camera is positioned further away.
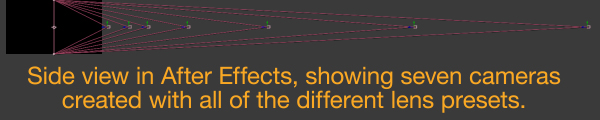
However if you open up the settings for an existing camera and choose a different preset, then After Effects doesn’t change the camera position. This means you can directly compare different lens types. So if you’ve already added a camera and have used the 50mm preset, then changing the camera settings will change the output – the 35mm preset will give you a wider view, while the 200mm preset will magnify the image significantly.
The After Effects camera settings
We can now look at what the camera settings are doing, and how After Effects works with the different parameters.
After Effects measures the focal distance of a lens in pixels, instead of mm.
Whenever a layer is the same distance from the camera in pixels as the focal length of the lens, it appears as 100% scale – in other words, it looks normal. Every time you create a new camera in After Effects, it automatically sets the z-position of the camera to be the same as the ‘zoom’.
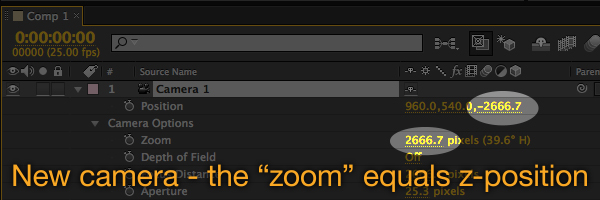
As layers move further away from the camera, they appear smaller. We can calculate the amount they need to be scaled up so that they appear the same size, by measuring the distance from the layer to the camera and calculating this as a percentage of the zoom – we’ll do this shortly.
Warm and Fuzzy
The camera settings in After Effects also include controls for depth of field. Depth of field refers to how much of a scene appears in focus, and in After Effects this can be turned on or off as needed.

If the depth of field setting is turned off then everything is always in focus. When turned on, the camera is “focused” at a particular distance – which can be controlled and animated – and layers appear blurrier the further away they are from the focus point.
In the real world, depth of field is controlled by the size of the lens aperture – to put it bluntly this is the size of the hole that lets the light in. The bigger the hole the smaller the depth of field – the fewer things are in focus. When the aperture is very small then the depth of field is said to be very large – in other words everything is in focus. Photographers measure apertures in F stops, and most real camera lenses have f-stops that range from about F4 to F22. Outside of this range – especially for the lower numbers – the lenses get very expensive, very quickly. Luckily, virtual cameras in software can easily have f-stops of less than 1 which is practically impossible in real life.
When taking photographs in the real world, the photographer is limited in choice by the amount of light available. There are many instances where the photographer might want to use a specific f-stop to achieve a desired depth of field, but there simply isn’t enough light available. The photographer has to balance creative intention with the technical requirements to actually take a photo that works. In other words, in the real world if a photographer gets the settings wrong then the photo won’t turn out – it might be too dark or too bright.
With virtual cameras in software, the exposure and light problems don’t exist, so the aperture control can be set to create the desired depth of field without have to worry about the amount of light available.
It’s also much easier to see the effect of the aperture as the setting is adjusted – so generally, the aperture setting can be dragged around and previewed in real time until you’re happy with the result.
Within the camera settings dialogue box, After Effects allows you to specify the aperture as an f-stop, but in the timeline the aperture is listed in pixels. There are formulas to calculate the depth of field based on the lenses focal length and aperture, but they’re outside the scope of this article.
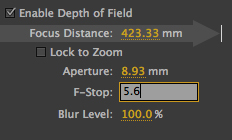
But basically – the larger the aperture, the more blurry the image.
Scale away, scale away, scale away
There are many applications where it’s useful to have a layer appear the same size, regardless of where it is positioned in 3D space. So let’s look at how the scale of a layer relates to the camera’s zoom and position. The numbers I’ve used here correspond to a 1920 x 1080 composition, and imagine that we have created a solid of the same size and made it a 3D layer. It’s z-position is 0.
When we create a new camera with the 50mm lens preset, After Effects converts this to a ‘zoom’ value of 2666.7 pixels. It also positions the camera with a z value of -2666.7 . Because our layer has a z position of 0, this means it’s 2666.7 pixels away from the camera. Because this is the same as the zoom value, the layer appears exactly the same size – 100%.

When a 3D layer is the same distance from the camera as the zoom value, it will appear the same size as a 2D layer at 100%.
If we move the 3D layer further away, it looks smaller – this is what you’d expect! If we make the layer’s z-position 3000, it’s now 5666.7 pixels away from the camera (2666.7 + 3000).
If we divide the new distance by the zoom value, we can get the distance as a percentage of the zoom.
(5666.7 / 2666.7) * 100 = 212.49%
If we take this value and use it to scale up the layer to 212.49%, then the layer again fills the composition and appears to be full size.
This works the other way, too. If we move the layer closer – eg with a z position of -500, then it is now 2166.7 pixels away from the camera. This works out as being 81.25% of the zoom value- and if we scale the layer to 81.25% then it appears the original size again.
We can use an expression to calculate the scale percentage dynamically, so that we can animate the layer and the camera without having to re-do the maths ourselves.
We’ll start with a simple example, and for the purposes of the example we’ll assume that the camera is called “camera 1”.
campos=thisComp.layer(“Camera 1”).toWorld([0,0,0]);
zoom=thisComp.layer(“Camera 1”).cameraOption.zoom;
lpos=thisLayer.toWorld(thisLayer.anchorPoint);
d=length(campos,lpos); // distance from layer to camera //
scl=(d/zoom)*100;
[scl,scl,100]
You can cut and paste this expression to the scale value of a 3D layer, and it will always appear to be scaled to 100% no matter how far away the camera is.
Maths, Maths Maths that’s all they ever think about
Within After Effects, the camera settings dialogue box shows you everything you need to know, and does all of the calculations and conversions for you. However when you get into scripting and expressions it can be useful to know how to do these conversions yourself.
There are three basic properties which are interrelated, and any two can be used to calculate the third:
– zoom (focal length in pixels)
– angle of view (in degrees)
– diagonal size (in pixels)
I noted earlier that one of the problems with describing a lens by its angle of view is that you also need to know which dimension is being measured. When it comes to the mathematics of lenses and optics, the diagonal is used.
We can use the Pythagorus theorem to calculate the diagonal length of the composition from the width and height of the composition. This is the simple C2=A2+B2 formula taught in high school, but we can write it here as an After Effects expression:
w=thisComp.width;
h=thisComp.height;
hyp=Math.sqrt((w*w)+(h*h));
As we know from high school, the term for the diagonal side of a triangle is the hypotenuse, so I’ve used the variable name hyp.
If we know the size of the diagonal and the angle of view, then we can calculate the focal length. In After Effects, the focal length is measured in pixels. I’ve had several instances where cameras imported from Maya have come in with the wrong zoom value, and if you know the angle of view of the camera in Maya then you can calculate the correct value in pixels for After Effects.
Because After Effects uses Javascript for expressions, we have to keep an eye on our use of degrees and radians. When working with cameras the angle of view is given in degrees, but trigonometry calculations in Javascript are done using radians. As we’ll be using the tangent and arctangent functions, we need to convert our angle of view into radians before we do the maths.
As an example, we’ll calculate the zoom value (the After Effects term for focal length) for a 50mm camera in a 1920 x 1080 composition. We know from the camera settings dialogue box that if we select the 50mm lens preset then the angle of view – diagonally – is 44.9 degrees.
w=thisComp.width;
h=thisComp.height;
hyp=Math.sqrt((w*w)+(h*h));
aov=44.9; // angle of view in degrees //
rad=degreesToRadians(aov/2); // convert to radians //
zoom=hyp/(2*Math.tan(rad))
[zoom]
If you try this yourself then you’ll see that the zoom value given is 2665.7, which is slightly different than the default value After Effects gives you of 2666.7. This is due to a small rounding error, as After Effects only gives us one decimal place for the angle of view. If we enter the angle of view as 44.885 instead of 44.9 then we get a result of 2666.7.
We can also convert the zoom value in After Effects to the angle of view in degrees. This is very useful if we have created and animated the camera zoom setting inside After Effects and want to translate the numbers to a different application (eg Maya) that defines the camera using the angle of view.
w=thisComp.width;
h=thisComp.height;
hyp=Math.sqrt((w*w)+(h*h));
zoom=2666.7;
aov=2*Math.atan(hyp/(zoom*2));
aov=radiansToDegrees(aov);
[aov]
If you try this, you’ll see that the value given for the angle of view is 44.885 degrees – a more precise value than the 44.9 degrees shown in the camera settings box.
This is also a good example of how it can be confusing to work with degrees and radians in expressions. In the first example, we started off with the angle of view that was described in degrees, so we had to convert it to radians before we called the tangent function.
In the second example, however, we use the arc tangent function but the value we input is not a measurement in degrees – it’s the ratio of the hypotenuse to the focal length. This ratio is not something that has been measured as degrees so there’s no need to convert it into radians. It is generally a pain in the proverbial to mix degrees and radians and in these situations we have to ensure we don’t get carried away and convert when we don’t have to.
Finally, if we know the zoom value and the angle of view then we can calculate the size of the hypotenuse, or the diagonal size of the composition. Because we’re starting with an angle of view that is measured in degrees, we have to convert the value to radians first.
zoom=2666.7;
aov=44.885;
rad=degreesToRadians(aov);
hyp=2*zoom*(Math.tan(rad/2));
[hyp]
Scale away – with feeling
Earlier we listed a simple expression that calculates the scale required to keep a layer at 100% size regardless of where the camera is positioned.
We can update this expression to take into account the layer’s scale, so that we don’t have to assume the layer is 100%. We can still scale a layer up or down and it will stay the same as the camera moves:
campos=thisComp.layer(“Camera 1”).toWorld([0,0,0]); // camera position //
zoom=thisComp.layer(“Camera 1”).cameraOption.zoom; // camera zoom //
lpos=thisLayer.toWorld(thisLayer.anchorPoint); // layer position //
lscl=thisLayer.transform.scale; // layer scale //
d=length(campos,lpos); // distance from layer to camera //
xscl=lscl[0];yscl=lscl[1];zscl=lscl[2];
x=(d/zoom)*xscl;
y=(d/zoom)*yscl;
z=(d/zoom)*zscl;
[x,y,z]
If this expression is applied to the scale property of a 3D layer, it will always appear the same size even when the camera changes position.
Expressions of interest
The virtual camera that was introduced with After Effects version 5 in 2001 has all of the same qualities as a real-world camera, even if some of the terms are slightly different.
For the After Effects expressioneer, or scripter, or just the merely curious, there are a few basic things to know to work with the camera more effectively.
– the lens presets in the camera settings dialogue box relate to 35mm photography. The 50mm preset is considered a normal lens.
– After Effects calls the focal length “zoom”, and measures it in pixels.
– when a new camera is created, After Effects automatically positions the new camera so it’s distance from the centre of the composition is the same as the “zoom” value.
– When a layer is the same distance from the camera as the “zoom” amount, it will appear the same as a 2D layer at 100%.
There are three main defining attributes that a virtual camera has – focal length, angle of view and diagonal size of the image plane – and any two can be used to calculate the third.
// Calculate the “zoom” (focal length) of a lens using the angle of view //
w=thisComp.width;
h=thisComp.height;
hyp=Math.sqrt((w*w)+(h*h));
aov=44.9; // angle of view in degrees //
rad=degreesToRadians(aov/2); // convert to radians //
zoom=hyp/(2*Math.tan(rad))
[zoom]
// Calculate the angle of view from the camera’s zoom value //
w=thisComp.width;
h=thisComp.height;
hyp=Math.sqrt((w*w)+(h*h));
zoom=2666.7;
// zoom = thisComp.layer(“Camera 1”).cameraOption.zoom; Alternatively get the value directly from the camera //
aov=2*Math.atan(hyp/(zoom*2));
aov=radiansToDegrees(aov);
[aov]
// Calculate the diagonal size of the image place from the camera’s zoom and the angle of view //
zoom=2666.7;
// zoom = thisComp.layer(“Camera 1”).cameraOption.zoom; Alternatively get the value directly from the camera //
aov=44.885;
rad=degreesToRadians(aov);
hyp=2*zoom*(Math.tan(rad/2));
[hyp]
// Automatically scale a 3D layer so it always appears the same size //
// Assume the active camera is called “Camera 1” – change accordingly //
campos=thisComp.layer(“Camera 1”).toWorld([0,0,0]); // camera position //
zoom=thisComp.layer(“Camera 1”).cameraOption.zoom; // camera zoom //
lpos=thisLayer.toWorld(thisLayer.anchorPoint); // layer position //
lscl=thisLayer.transform.scale; // layer scale //
d=length(campos,lpos); // distance from layer to camera //
xscl=lscl[0];yscl=lscl[1];zscl=lscl[2];
x=(d/zoom)*xscl;
y=(d/zoom)*yscl;
z=(d/zoom)*zscl;
[x,y,z]
Filmtools
Filmmakers go-to destination for pre-production, production & post production equipment!
Shop Now













